primal - PRIMe Algorithm tester Lite
NOTE: The prime number algorithms tested
with this program are described in greater detail in
"Primality Testing".
primal
does various things with prime numbers. It's heavyweight sibling,
primate, was written to test my
prime-number functions in LIBGPL's
NBR_UTIL package.
This lightweight version strips a lot of the comparative functionality,
specifically the handful of alternative variants of the NBR_UTIL
nbrIsPrime() function, which is now used exclusively.
My hope is that primal will run on my Palm Pilot
(emulator) — the emulator has an immediate, fatal error
when SioMain() calls primate's main().
(Update: Both programs work on the Palm Pilot. The ".prc" files
I just tried date back to 2019, so I must have figured out what the
problem was.)
Basic Usage
Check if a number is prime:
% primal number
List all primes in the range, [start...end], inclusive:
% primal -list start-end
List count primes beginning with start:
% primal -list start,count
Find the next prime after a number (even if the number itself is prime):
% primal -next number
Verify that the prime functions generate the correct primes in 3 ranges.
The generic "-verify last" option chooses the appropriate bit width for the
CPU's unsigned longs. The pre-computed tables against which generated
primes are matched have entries for 32- and 64-bit unsigned longs. If
unsigned longs are less than 32 bits wide, there's no point in trying
"last32" verification. Likewise, if unsigned longs are less than 64 bits
wide, there is no point in trying "last64" verification.
% primal -verify first # First 1000 prime numbers.
% primal -verify last # Last 1000 prime numbers in unsigned long.
% primal -verify last32 # Last 1000 prime numbers in 32-bit integer.
% primal -verify last64 # Last 1000 prime numbers in 64-bit integer.
Advanced Usage
Time an operation; most output is suppressed in timing mode. If the
operation is very quick, repeat the operation count times to get
meaningful times for comparison purposes.
% primal -time [-repeat count] ... (other options) ...
Select a different skip-through prime for the default nbrIsPrime();
the default is STP 7. This option also generates the sequence of
differences for the new skip-through prime; the often lengthy time
taken to generate a sequence is not included in timing benchmarks ("-time").
% primal -qprime stp ... (other options) ...
Print information (sequence length, range, etc.) about all skip-through
primes that can be used without overflow according to the size of an
unsigned long:
% primal -qinfo
Print the same information for 128-bit unsigned integers (using a GCC
extension for 128-bit integers which is only used in this program
for generating this information):
% primal -q128info
List the sequence of differences for a skip-through prime:
% primal -qgen stp
Rarely used options not discussed here: "-qc#kpi stp" and "-qmax
stp".
Invocation:
% primal [-debug] [-help]
# Operations
[-list start]
[-list start,[-]count]
[-list start-end]
[-maximum 32|64]
[-next number]
[-qc#kpi stp] [-qgen stp] [-qmax stp]
[-qinfo] [-q128info]
[-verify first|last|last32|last64] [-xtra]
[number]
# Modifiers
[-qprime stp]
[-repeat count] [-time]
where
-debug
- turns debug on.
-help
- prints out a help message.
-list start
-list start,[-]count
-list start-end
- generates a list of prime numbers. If "start" alone is
specified, the program generates prime numbers beginning at the
start number (which may or may not be prime itself); the program
will continue running until ULONG_MAX is reached and checked.
If "start,count" is specified and count
is negative, the last count prime numbers preceding and
ending with start are generated (in reverse order). If
count is positive, the first count prime numbers
beginning with and following start are generated. If a
range is specified, "start-end", the program
will generate a list of the prime numbers in that range, including
the start and/or end numbers if they're prime.
-maximum 32|64
- checks if the pre-computed, largest 32- or 64-bit prime numbers
are prime (which, of course, they are). "primal -max 64" takes
nearly 40 seconds on my old, Fedora Core 15 computer to test
the primality of the largest 64-bit prime (using the default
skip-through prime of 7).
-next number
- prints out the next prime number after the given number, regardless
if the given number is itself prime.
-qc#kpi stp
- generates a listing of the values of i coprime with c#,
where c is the specified skip-through prime. These values are
associated with the c#k+i form for primes; see
the file prolog in nbr_util.c for a detailed description. The program
derives the values of i from the skip-through prime's sequence
of differences, so the same memory and time constraints of the
"-qprime stp" option apply. (The "p" in "c#kpi" means
"plus", i.e., "c#k+i".)
-qgen stp
- generates and lists the sequence of differences for skip-through
prime stp. This operation requires allocating memory
for the sequence of differences. My computer (64-bit Linux)
successfully allocated the 1GB sequence for STP 29, but failed
when trying to allocate the 30GB sequence for STP 31. Large
skip-through primes have long sequences, so be aware that the
output of this option can be voluminous; for example, one billion
numbers are listed for STP 29.
-qmax stp
- determines the maximum difference in the sequence of differences for
skip-through prime stp. The algorithm used is identical to
the algorithm used by "-qgen stp", but it is not necessary to
allocate memory for the sequence. As each difference is generated,
it is compared to the maximum seen so far and then discarded.
Consequently, this operation is useful as a stand-in for
"-qgen stp" when benchmarking sequence generation for
skip-through primes whose sequences require more memory than the
system can allocate. Be aware that this is a time-consuming process
for larger skip-through primes. On my computer, it took 11
seconds — at 100% CPU usage — to scan the
differences for STP 23, nearly 7 minutes for STP 29, 3.5 hours for
STP 31, and 6.4 days for STP 37!
-qinfo
- displays a table of the characteristics of all possible skip-through
primes and their sequences of differences, given the size of unsigned
longs on the CPU.
-q128info
- displays a listing of the characteristics of all possible skip-through
primes and their sequences of differences for 128-bit, unsigned
integers. (The numbers are very, very big, so a table was out of the
question.) This option takes advantage of GCC's (and others')
non-standard implementation of 128-bit arithmetic on 64-bit CPUs.
This option is only available if C preprocessor symbol HAVE___INT128
is defined as 1 when this program is compiled with GCC. This GCC
extension for 128-bit integers is not used elsewhere in
the program or in the NBR_UTIL library. So, the checking, listing,
and verifying of 128-bit integers is not supported (unless the CPU's
"unsigned long" data type is actually 128 bits wide).
-verify first|last|last32|last64
- verifies that the prime function generates the correct prime numbers
in certain ranges. The verification immediately terminates with an
error message if a non-prime number is generated or if an actual prime
number is skipped. The generated prime numbers are compared to one of
the tables of pre-computed primes in 3 ranges:
- "-verify first" verifies the first 1000 prime numbers.
- "-verify last" verifies the last 1000 prime numbers that can
be represented in an unsigned long. If the width of an
unsigned long is 64 bits or greater, the last 1000 prime
numbers preceding 264 are verified. If the width
is less than 64 bits, the last 1000 prime numbers preceding
232 are verified.
- "-verify last32" verifies the last 1000 prime numbers preceding
232; this option is also useful if the native
unsigned longs are wider than 32 bits (e.g., 64 bits).
NOTE that "-verify last" on a CPU with 64-bit longs takes
a very long time. On my old Fedora Core 15 machine, 24.8 hours to
be exact!
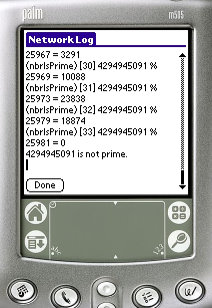
-xtra
- checks if 4294945091 is prime (it isn't). A shorthand option for me
when I was developing this program.
number
- checks if the given number is prime.
-qprime stp
- specifies the skip-through prime to use with the library function,
nbrIsPrime(). To use the desired skip-through prime,
the "-qprime stp" option must generate the sequence
of differences for the STP. On my computer, it took 11 seconds to
generate the sequence for STP 23 and nearly 7 minutes for STP 29.
The system couldn't allocate enough memory for STP 31's sequence,
but it would take 3.5 hours to generate STP 31's sequence and
6.4 days to generate STP 37's sequence!
-repeat count
- repeats certain operations the specified number of times. This is
useful, for example, when timing checking if a number is prime.
A single check might take too little time to make a meaningful
comparison with, say, an alternate is-prime? function;
repeat the check 1,000 times or 10,000 times and a more realistic
comparison can be made.
-time
- measures and displays the time it takes to perform an operation (or
count iterations of the operation if "-repeat count"
is also given on the command line). Almost all output is suppressed
to keep I/O from affecting the timing. If the "-qprime stp"
option was specified, the skip-through prime's sequence of differences
is generated before the timer is started.

